Who has the best forehand and backhand in men’s tennis? In this post, I make a first attempt at tackling this question using data from the Match Charting Project (MCP).

The idea

The fundamental idea is to look at a single shot at a time. Say Federer hits a forehand off a Djokovic backhand. One of three things can happen: Federer (1) returns the shot, (2) hits a winner, or (3) makes an error. I am not distinguishing unforced and forced errors here to keep it simple.

When considering the likely outcome, there are some important factors. Of course the outcome will be driven in part by Federer’s skill on the forehand. But the opponent also plays a role: the incoming backhand shot may put Federer under pressure. And it’s likely that it’s harder to hit a winner against Novak than against most other players. So, my current model looks roughly like this: \(z = \textrm{shot_quality} + \textrm{incoming_shot_quality} + \textrm{opponent_defense} + \textrm{intercept}\)

Model details

Feel free to skip this section if you’re not interested in the details! The scores $z$ here are the log odds relative to the base outcome (“returned”). The log odds are given by:

\[z_{\textrm{outcome}} = \log \frac{p(\textrm{outcome})}{p(\textrm{base class})}\]

If an outcome is as likely as the base class, then $z_\textrm{outcome} = 0$; if it’s less likely, it’s negative, and if it’s more likely, it’s positive. The base class is fixed at $z = 0$, since $z_{base} = \log 1 = 0$. This kind of model is called a “Multinomial logit”; If you’d like to read more, here’s a good introduction.

To make things more concrete, let’s look at Federer hitting a forehand off a Djokovic backhand as an example. The intercept for a forehand is -2.72 for winners, and -1.53 for errors. Adding the zero log odds for the base class, the complete $z$, as a vector, is equal to $[0, -2.72, -1.53]$. To turn this into probabilities, this vector is passed through the softmax function to give 78% probability of shot being returned, 5% probability of a winner, 17% probability of an error.

Federer’s shot quality addition is 0.37 for winners, and 0.15 for errors. So he raises the log odds of winners by 0.37 to -2.35, and the log odds for errors to -1.38. So, against an average player, we’d expect Federer to return the ball 74% of the time on his forehand, hit a winner 7% of the time, and make an error 19% of the time.

How does playing Novak affect things? It turns out that Novak reduces the log odds of hitting a winner off a forehand by 0.18, and leaves the error probability unaffected. Also, Novak’s incoming backhand reduces the log odds of hitting a winner by 0.25, and the chance of an error by 0.11. Putting all this together, the log odds for the winner are -2.78, and the error -1.49, so we’d expect Federer’s forehand to be returned 78% of the time, a winner 5% of the time, and an error 18% of the time. As you’d expect, it’s harder to hit winners against Novak!

One more detail: I won’t explain this in any depth here, but I also make an attempt to correct for the sample of the MCP using post-stratification. I might talk about this more in a future post, but I think there is already plenty of detail in this one for now.

Calculating shot quality from the model

Having estimated these coefficients, how can we find the player with the best forehand and backhand? I think a neat way to go is to consider a duel: if a player gets into a forehand-forehand duel with an average player, how often are they expected to come out on top? Using all matches charted for hard courts since 1990 and limiting the players to those with at least 10 matches charted, we can do this and produce the following plot:

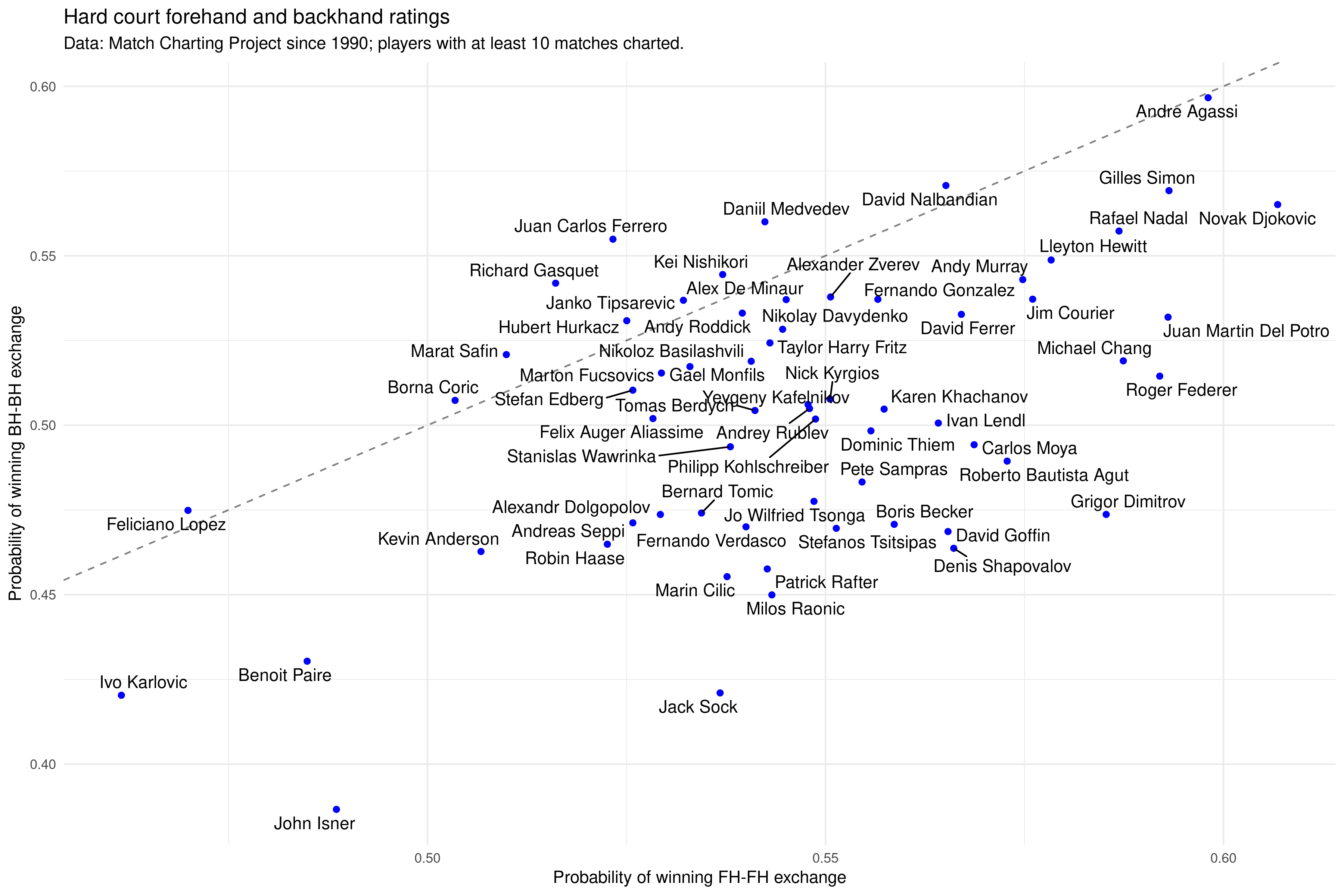
Here are some notes on the plot:

• The dashed line is the line of equal skill on forehand and backhand. Most players lie below, which means they’re more likely to win a forehand exchange than a backhand exchange. But there are some players that lie above the line, like Gasquet and Medvedev, whose backhands are better than their forehands. I was a little surprised to see Ferrero there, too, but I haven’t seen him play too much, so maybe that’s fair.
• The top right corner has the best baseliners. Andre Agassi takes the crown in this analysis. His backhand and forehand are rated extremely highly. In fact, he is estimated to have the best backhand: he’s expected to win almost 60% of baseline backhand-backhand rallies. Novak Djokovic is also extremely highly rated on both the forehand and backhand, as is Nadal and, perhaps surprisingly, Gilles Simon!
• The players below the line have better forehands than backhands. Federer and Del Potro stand out on the right end here, having some of the best forehands and good, but not great, backhands. Dimitrov is in this camp too, interestingly; his one-hander is flashy but perhaps not that effective.
• Big servers Karlovic and Isner stand out as being poor baseliners and are expected to lose most of their rally exchanges against the average player, be it forehand-forehand or backhand-backhand. Raonic and Anderson do somewhat better, perhaps explaining their greater career success.
• Fernando Gonzalez, a personal favourite, is pretty high in the forehand ratings, but it’s not among the very best. I suspect that this is because he took a lot of risks on his forehand, so while he hit a lot of winners, he’d do so at the cost of some errors, too. I’m planning to look into that in a future post.
• I’ll admit that the plot is not without surprises. Some I think hold up. For example, Gilles Simon might indeed have excellent ground strokes, but his serve is terrible, so that may be why he hasn’t been as successful as the other players in his group. Others are a bit more surprising, like Lopez’s backhand being rated to be on par with his forehand. That doesn’t mesh with conventional wisdom: Lopez’s backhand is generally thought of as being terrible, while his forehand is considered quite dangerous. Either his backhand isn’t as bad as people think it is, or perhaps there is some other problem here.
• I want to emphasise that this plot tells only part of the story, because the serve is not considered. This hurts players like Sampras, for example, who doesn’t look great on this plot.

Summary

In summary, I hope you’ve enjoyed this first look at my attempt to rate player’s shots with the MCP. I’ll admit that I am not entirely sure about some of the modelling decisions I’ve made yet, and whether my adjustments to the sample are adequate. Nevertheless, I wanted to share the results, and I hope the plot could lead to plenty of interesting discussions!